
기체의 운동 분자 이론은 기체 분자가 차지하는 부피와 분자 사이의 모든 상호작용을 무시한다는 가정에서 출발하고 있어, 실제로는 모든 기체는 0이 아닌 분자량을 가지고 있고, 또한, 실제 가스의 분자들은 분자의 구조에 따라 달라지기 때문에 실제기체와 차이가 있어 그에 대해 살펴보고자 한다.
이상기체 vs. 실제기체
이상기체 (Ideal gas)
이상기체는 다음의 성질을 만족한다고 가정한다.
2. 무작위적인 운동, 즉 방향이 정해지지 않은 운동을 하며, Newton의 운동법칙을 따른다.
3. 각 입자의 총 부피는 기체 전체가 차지하는 부피에 비해서 무시할 수 있다. 즉, 기체 입자는 점질량이다.
4. 충동하는 시간을 제외하면, 분자에 작용하는 힘은 무시해도 좋다. 즉, 인력 및 반발력이 없다.
5. 충돌은 (완전)탄성충돌이며, 충돌에 걸리는 시간은 무시할 수 있다.
완벽한 기체 법칙은 상태 방정식의 한 예이다.
상태 방정식을 시각화하는 한 가지 방법은 T의 고정 값에서 P 대 V의 그래프인 소위 등온성을 나타내는 것이다.
다음 그림 1은 이상 기체 방정식 P=nRT/V를 여러 등온을 기준으로 시각화한 P-V 그래프이다.

<그림 1> Pressure vs. volume for different temperatures (isotherms) of the ideal-gas Equation of state.
여기서 주목해야 할 것은 이상적인 기체는 오직 기체로만 존재할 수 있다는 것이다. 이상적인 기체가 일종의 "이상적인 액체"로 응축되는 것은 불가능하다. 즉, 입자 간 상호작용이 적절히 설명되어야 기체에서 액체로의 위상 전이를 모델링할 수 있다.
압축성 인자 Z (compressibility factor)
특정한 기체의 거동이 이상기체의 행동으로부터 얼마나 벗어나는지에 대한 척도로 압축성 인자 Z를 정의한다.
- 이상기체 :

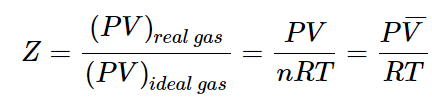
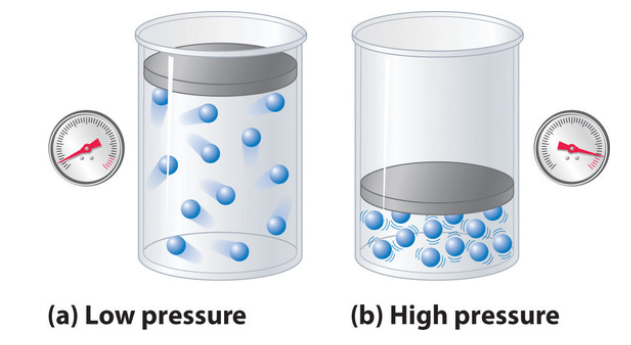
왼쪽 그림은 고압에서 실제 가스의 비이상성을 보여주는데, 상대적으로 낮은 압력에서 액화되는 C2H4와 CO2가 음의 편차가 크게 관찰된다.
오른쪽 그림은 충분히 낮은 압력(따라서 낮은 밀도)에 대해 각각의 실제 기체가 예상대로 이상 기체 거동에 접근한다는 것을 보여준다.

<그림 2> Two graphs of the compressibility factor (Z) vs. pressure at 273 K.
그 결과, 분자가 차지하는 부피는 용기의 부피와 비교하여 의미가 달라진다. 결과적으로, 기체가 차지하는 총 부피는 이상 기체 법칙에 의해 예측된 부피보다 커지게 되어, 매우 높은 압력에서 실험적으로 측정된 Z 값은 이상 기체 법칙에 의해 예측된 값보다 크다.
| 압축성 인자 Z (compressibility factor) - 임의의 온도, 압력의 상태에 있는 특정기체 1mol의 부피(Vm)와 동일한 조건에 있는 이상기체의 부피(Vm_i)와의 비 Z = 실제기체의 몰부피 / 이상기체의 몰부피
= Vm / Vm_i = pVm/(RT) |
이상기체(Ideal das) 같은 경우에는 Vm 과 Vm_i 이 같기 때문에 언제나 Z=1이다.
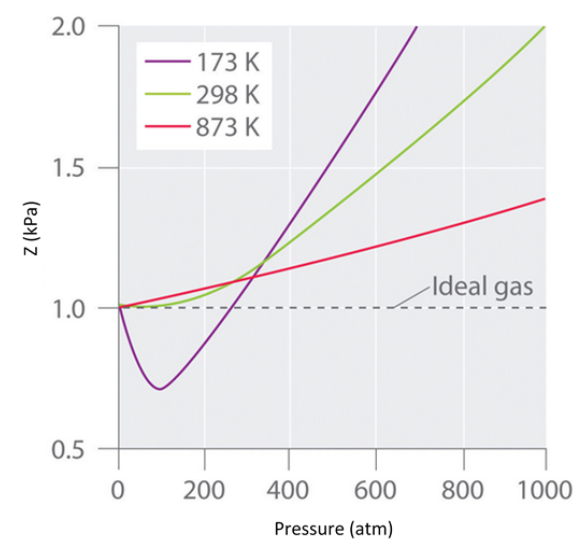
Z=1로부터 얼마나 벗어나는지를 측정한 그래프이다. 0atm에서 압력이 커질수록 Z<1이 되는데 이때는 실제 부피가 이상기체의 부피보다 작다는 것을 의미하며 인력이 우세하다는 뜻이다.
그런데 높은 압력에서는 Z>1이 되는데 이때는 실제 부피가 이상기체의 부피보다 크다는 것을 의미하며 반발력이 우세하다는 뜻이다.
Z≒1 인 부분은 이상기체와 비슷한 이상적 행동을 하는 부분이다.
비리알 계수(Virial coefficients)
이상기체 법칙은 실제기체에 대한 불완전한 설명이기 때문에, 우리는 완벽한 기체 법칙과 실제 기체의 압축성 요소를 결합하여 실제기체를 설명하는 방정식을 생각할 수 있다.
즉, 실제 기체가 이상기체의 거동과 약간의 차이가 있어, 약간씩 벗어나는 것을 맞추기 위해서 밀도의 거듭제곱의 표현한 비리알 상태식 (Virial equation of state)이 만들어 졌고, 이상기체 상태식은 다음 형태의 식들의 첫째항만으로 나타낸 것이다. 무한급수로 표현되는 비리알 상태식과는 당연히 오차가 생기는데, 그 오차가 실제기체와 이상기체의 차이를 의미한다.

여기서,
- B is the second virial coefficient,
- C is called the third virial coefficient, etc.
또한, ρ = n/V 으로서 다음과 같이 표현된다.

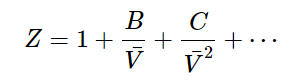

<그림 5> 이산화탄소의 등온선
위 그림 5는 이산화탄소의 부피의 변화에 따른 압력의 변화를 나타낸 것이다.
Vm이 크고 높은 온도(50℃)부근에서는 Boyle의 법칙과 거의 유사하다. 그러나 잘 맞는 것이지, Boyle의 법칙을 완벽하게 따르는 것은 아니다. 이것은 실제 기체가 이상기체의 거동과 약간의 차이가 있는다는 것을 의미한다.
즉, 약간씩 벗어나는 것을 맞추기 위한 것이 비리알 상태식 (Virial equation of state)이다.
임계 상수(Critical constant)
임계점이란 위 그림 5에서 액체부분인 점 W 와 기체부분인 점 V를 연결하는 수평선이 특정한 온도(임계 온도, critical temperature, Tc)에서 한점으로 합쳐지는 부분이다.
이때의 압력을 임계 압력(critical pressure, pc), 몰 부피를 임계 몰부피(critical molar volume, Vc)라고 한다.
그리고 pc, Vc,Tc 들을 임계 상수(critical constant)라고 부른다. 따라서 Tc 보다 낮은 온도의 등온 곡선은 기체에 압력이 가해지면 액체로 되는 응축점이 존재하나 Tc 보다 높은 온도의 등온 곡선에서는 이러한 응축점이 존재하지 않는다. 따라서 액체와 기체를 구분할 수 있는 두 상간의 경계점이 생기지 않는다. 즉 Tc 보다 높은 온도에서는 압축에 의하여 응축에 의한 액체를 만들 수 없음을 뜻하는 것이다.
그리고 이러한 유체를 초임계 유체(critical fluid)라고 부른다.
Reference : 1. https://joonyoungsun.tistory.com/entry/분자-상호작용
2. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps
'공학 기술 > 공학기본' 카테고리의 다른 글
| 열역학 제1법칙 (0) | 2021.12.18 |
|---|---|
| 정압비열 vs. 정적비열 (0) | 2021.12.05 |
| 상태량 표(열역학 성질표) (0) | 2021.12.03 |
| 상변화 과정에 대한 상태량 선도 (0) | 2021.12.01 |
| 순수 물질의 상변화 과정 (0) | 2021.11.30 |





댓글