스팀 가열 시스템에서 스팀의 생성 및 공급의 목적은 주로 공정의 열 전달면에 열을 공급하기 위한 것이다. 필요로 하는 열량과 스팀 압력을 안다면 이에 필요한 스팀 사용량을 결정할 수 있다. 아울러 보일러 및 스팀 공급 시스템의 크기도 결정할 수 있다.

Heat Transfer(열 전달) 식
대부분 실제 상황에서는 모든 에너지가 한가지 형태의 열 전달만으로 전달되지 않는다.
전체 열 전달 과정은 통상 두 개 혹은 더 다양한 메커니즘이 결합되어 있다. 설계 단계에서 전열면을 통과한 열 전달량을 계산하기 위해 사용되는 일반적인 식은 아래와 같다.
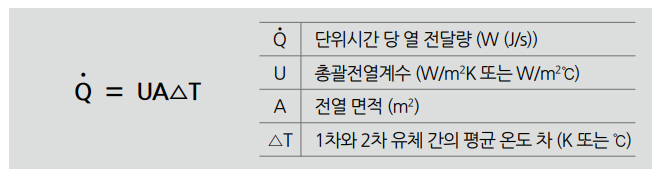
상기 방정식으로부터 우리는 U값이 열 전달량인 Q에 직접적으로 비례 한다는 것을 알 수 있다. 전열 면적과 온도차가 변하지 않는다고 가정하면 U값이 클수록 열전달량이 커진다. 다시 말하자면 같은 설비이더라도 U값이 클수록 소요 시간이 단축될 수 있다.
총괄전열계수 (U)
이것은 고체의 전열면에 의해 분리되는 두 개의 유체 사이의 전도 및 대류 저항을 고려한 것이다. 총괄전열계수는 열 전달에 대해 각각의 열저항의 합인 총괄열저항의 역수이다.
 |
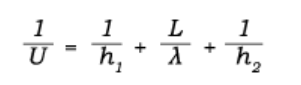 |
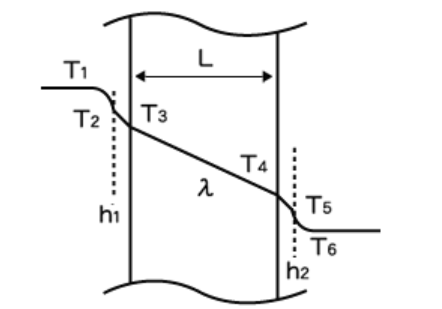
| h = 대류 열전달 계수, W/(m°C) L = 열전달면의 두께, m λ = 열전도도, W/(m°C) |
<그림 1> 금속의 열 전달면을 통한 열 전달
<대류 열전달 계수(h)>
대류 열전달 계수(h), 때로는 경막 계수라고도 하며 유체와 고체 사이의 열전달을 계산할 때 자주 사용된다. 열교환기의 경우 열전달은 기본적으로 유체1(열원)에서 고체(열전달면)에서 유체2(피가열물)까지 발생한다. 열전달이 여러 고체를 통해 발생하는 경우 위의 방정식은 고체의 두께(L)를 열전도도(λ)로 나눈 값을 보완하여 적용할 수 있다.
계산을 단순화하기 위해 다음 값을 대류 열전달 계수에 대한 참조로 사용할 수 있다.
<표 1> 유체의 대류 열전달 계수
| 유체 | 대류 열전달 계수(h) |
| 물 | 약 1000 W/( ㎡ °C) |
| 온수 | 1000 – 6000 W/( ㎡ °C) |
| 증기 | 6000 – 15000 W/( ㎡ °C) |
총괄전열계수는 또한 열 전달 과정에서 오염의 정도를 고려할 수 있다. 열 전달 표면의 필름막 또는 스케일의 침적은 상당한 정도로 열 전달량을 감소시킨다. 오염 계수는 유체와 벽 사이에 발생하는 유체의 불순물, 녹 형성물 혹은 기타 반응물에 의해 야기되는 추가적인 열저항을 나타낸다. 각각의 전열계수의 크기는 열 전달 과정, 유체의 물리적 특성, 유체의 유량 및 열 전달 표면의 물리적 형태에 따라 다르다. 열교환기 배열은 열 전달 면적이 결정되어야 정할 수 있기 때문에 열교환기의 디자인은 필연적으로 반복적인 절차를 형성하게 된다. 이러한 절차를 위한 출발점에서는 통상 다양한 유형의 열교환기의 총괄전열계수에 대해 대표값을 선택한다. 각각의 전열계수에 대한 정확한 계산은 그 복잡한 절차 때문에 대부분의 경우 일부의 알려지지 않는 변수로 인해 불가능하다. 따라서 확립된 총괄전열계수의 대표값을 사용하면 실무적인 목적에 적합하다.
온도차 (△T)
뉴튼의 냉각 법칙은 열 전달량이 온도가 높은 매체와 낮은 매체간의 온도 차와 관계가 있음을 말한다. 열 전달 과정에서 이러한 온도차는 위치 혹 은 시간에 따라 변화하게 된다. 일반적인 열 전달 식은 뉴튼의 냉각 법칙 의 확대 개념으로 발전된 것이며, 이 경우 평균 온도차는 주어진 열량을 만족시키기 위해 필요한 전열 면적을 확정하기 위해 사용된다.
평균 온도차 (△T M)
열교환기와 같은 흐름 형태 과정에서의 평균 온도차의 계산은 흐름의 방향에 따라 다르다. 1차 및 2차 유체는 동일한 방향(병류 / Cocurrent flow), 반대 방향(Countercurrent flow), 또는 상호 교차 방향(Crossflow)으로 흐를 수 있다. 포화증기를 사용할 경우, 1차측 유체의 온도는 열이 상(Phase) 변화만의 결과로서 전달되기 때문에 일정할 수 있다. 그 결과 온도 분포는 유체 흐름 방향에 따라 더 이상 변화지 않게 된다. 그러나 2차측 유체가 열 전달 표면을 스쳐가기 때문에 최대의 열 전달량은 인입부에서 발생하게 되며, 점차 그 통로를 따라 토출부에 이르러서는 감소된다. 이것은 단순히 스팀과 2차측 유체 사이의 온도차가 2차측 온도의 상승으로 인해 감소되기 때문이다. 스팀 및 2차측 유체의 온도 변화의 결과치는 대표적으로 그림 2와 같이 나타난다.
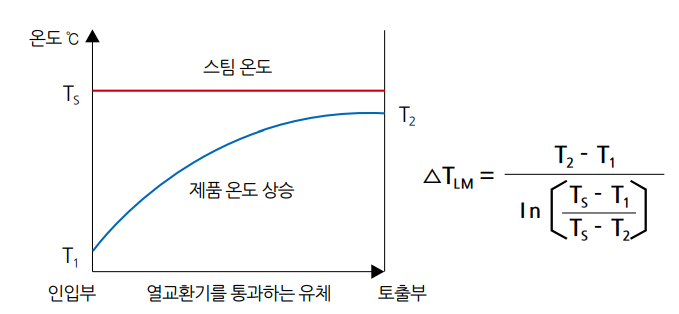
<그림 2> 대수평균 온도차 (LMTD)
2차측 온도의 상승은 비선형으로서 대수적 계산 방법에 의해 잘 표현될 수 있다. 이러한 목적을 위해 선택된 평균 온도차를 대수평균 온도차 혹은 LMTD 또는 ∆TLM로 표시할 수 있다.
평균 온도차를 산출할 수 있는 더욱 쉬운(그러나 정확도는 떨어지는) 방법은 산술평균 온도차 혹은 AMTD나 ∆TAM을 이용하는 방법이다. 이 것은 2차측 유체 온도가 선형적으로 증가하는 것을 가정하는 것으로서 편의상 대략 만족할 만한 평균 온도차를 사용할 수 있다. AMTD 온도 변화는 그림 3에서 설명되는 바와 같다.
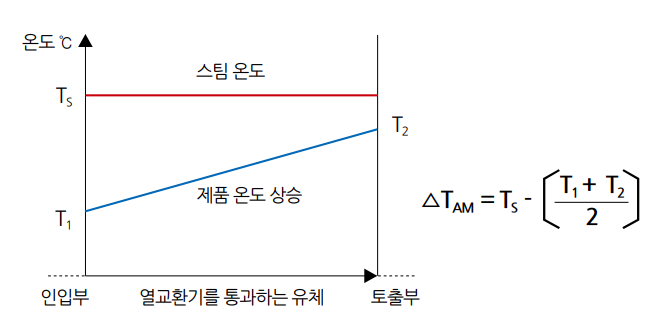
<그림 3> 산술평균 온도차 (AMTD)
Reference : 1. Spirax sarco, Steam People Vol. 125(Sep, 2020)
'공학 기술 > 공장설계' 카테고리의 다른 글
| Breather Valve 배출량 (1) | 2023.12.29 |
|---|---|
| Steam 소비량 추정 (0) | 2023.12.18 |
| 제어풍속 vs. 반송속도 (0) | 2023.11.15 |
| CO 경보기 설치위치 (0) | 2023.09.17 |
| 안전장치 소요 분출량(에너지법) (0) | 2023.09.17 |





댓글