화학 공장에서 발생하는 대부분의 사고는 독성, 인화성 또는 폭발성 물질의 누출되어 발생하는 경우가 많다. 이럴 경우 누출공을 통한 누출량 계산이 필요하여 이에 대한 내용을 공유하고자 한다.

구멍을 통한 증기·가스의 누출량
가스 및 증기의 배출
일반적으로 흐르는 액체의 경우 비압축성 유체(incompressible liquids) 운동 에너지 변화는 무시할 수 있는 경우가 많으며 물리적 특성(특히 밀도)은 일정하다.
그러나 흐르는 가스 및 증기와 같은 압축성 유체(compressible liquids)의 경우 이러한 가정은 작은 압력 변화(P1/P2 < 2)와 낮은 속도(기체 음속의 0.3배 미만)에 대해서만 유효하다. 즉 가스 또는 증기에 포함된 에너지는 압력의 형태로 나타나며, 가스 또는 증기가 구멍을 통해 빠져나가거나 팽창할 때 운동 에너지로 변환된다. 가스 또는 증기가 누출 구멍을 통해 빠져나가면서 밀도, 압력 및 온도가 변화한다.
가스 및 증기 방출은 교축(絞縮, throttling)* 방출과 자유 팽창(free expansion) 방출로 분류된다.
* 교축 Throttling : 유체의 유동 중 팽창밸브나 오리피스, 모세관 등에 의해 유동의 단면이 줄어들 때 유체는 단열상태에서 외부와 열량이나 일량의 교환없이 압력강하만 일어나는 현상을 말한다.
※ 교축 방출의 경우 마찰 손실이 큰 작은 균열을 통해 가스가 방출되며, 가스 압력에 내재된 에너지 중 운동 에너지로 변환되는 에너지는 거의 없다.
※ 자유 팽창 방출의 경우 대부분의 압력 에너지가 운동 에너지로 변환되며, 일반적으로 등엔트로피(isentropic) 거동에 대한 가정이 유효하다.
누출모델(Source model)
교축 방출 누출 모델에는 누출의 물리적 구조에 대한 자세한 정보가 필요하므로 여기서는 고려하지 않고, 누출 물리적 구조 정보 중 누출의 직경의 영향을 받는 다음 그림과 같은 자유 팽창 누출(free expansion leak)에 대해서만 검토한다. 또한 일반적 사고의 경우도 대부분 자유 팽창 누출의 경우이다.

<그림 1>자유 팽창 가스 누출
기체는 누출공을 통해 등엔트로피 팽창을 한다. 팽창하는 동안 기체 특성(P, T) 및 속도가 변화한다.
등엔트로피 팽창 질량 유량식
상기 그림에서 아래 첨자 "o"로 표시된 초기 점(initial point)과 아래 첨자 없이 표시된 임의 최종 점(arbitrary final point )에서의 압축성 가스 및 증기 흐름의 mechanical energy balance를 살펴보자.
두 점간의 전위 에너지 변화가 미미하고 샤프트 작업이 없다고 가정하고, 속도가 0이고 압력이 P인 초기 점(아래 첨자 "o"로 표시)이 선택되며, 임의의 최종 점(아래 첨자 없이 표시)까지 mechanical energy balance를 적분하면 다음 식을 얻을 수 있다.
(식 1)

압축성 가스 및 증기 흐름의 mechanical energy balance에서 두 지점간의 전위 에너지 변화가 미미하고 샤프트 작업이 없다고 가정하고, 속도가 0이고 압력이 P인 초기 점(아래 첨자 "o"로 표시)이 선택되며, 임의의 최종 점(아래 첨자 없이 표시)까지 적분이 완료되면 다음과 같다.
isentropic expansion(등엔트로피 팽창)을 겪는 모든 이상 기체의 경우, 다음 식이 적용된다.
(식 2)

여기서 γ는 열 용량의 비율, γ = Cp/Cv 이다.
따라서 등엔트로피 팽창에서 어떤 지점의 유체속도를 얻기위해 방정식 2를 방정식 1에 대입하고 새로운 배출 계수 Co를 정의(기 포스팅한 구멍을 통한 액체의 누출량 식 4 참조)한 후 적분하면 다음과 같은 방정식이 나온다:
(식 3)

이 식에서 초기 밀도 ρo에 이상기체 법칙을 적용한 형태이다.
등엔트로피 팽창에 대한 이상 기체 법칙을 사용하면 다음과 같다.
(식 4)

연속성 방정식(continuity equation) Qm = ρuA에 방정식 4와 방정식 3을 사용하면 다음의 질량유속에 대한 식이 얻어진다.
(식 5)

방정식 5는 등엔트로피 팽창 도중 어떤 시점에서의 질량 유량을 나타내고 있다.
쵸크(choked) , 임계(critical) , 음속(sonic) 흐름
많은 안전 연구에서는 구멍을 통한 증기가 누출되는 것에 관련된 문제를 해결하기 위해 통과하는 증기의 최대 유량이 요구된다.
이는 방정식 5를 P/Po로 미분하고 그 미분값을 0으로 설정하면 얻어진다. 그 결과 최대 유량을 초래하는 압력 비율은 다음과 같다:
(식 6}

쵸크 압력 (choked pressure), Pchoked는 구멍 또는 파이프를 통해 최대 흐름의 결과로 나타나는 최대 하류 압력(maximum downstream pressure)이다.
하류압력이 Pchoked 미만의 경우 다음과 같은 상황설명이 유효하다.
(1) 누출구에서 유체의 누출속도는 일반적인 조건에서 음속이며,
(2) 속도와 질량 유량은 다운스트림 압력을 감소하더라도 더 늘릴 수 없으며 downstream 조건과 무관하다.
이러한 유형의 흐름을 초크(choked) 흐름, 임계(critical) 흐름 또는 음속(sonic) 흐름이라고 하며 그림 2에 예시하였다.

<그림 2> 구멍을 통한 가스의 쵸크 흐름.
기체 속도는 누출공에서 음속과 같다. 질량 유량은 다운스트림 압력과 무관하다.
열 용량 비(heat capacity ratio) γ
방정식 6의 흥미로운 특징은 이상적인 가스의 경우 크 압력은 열 용량 비율 γ의 함수라는 점이다.
그리고 이상 기체의 열용량비( γ )는 분자의 자유도( f )와 다음과 같이 연관될 수 있다:
| Relation with degrees of freedom | Gas | degrees of freedom | heat capacity ratio ( γ ) |
 |
monatomic | 3 | |
| diatomic | 5 |
* 예시: 공기(air)는 주로 이원 기체(질소(N2) ~78%, 산소(O2) ~21%)로 구성되어 있으며, 표준 조건에서는 이상적인 기체로 간주할 수 있다. 이원자 분자는 5개의 자유도(3개의 병진 자유도와 2개의 회전 자유도, 진동 자유도는 고온을 제외하고는 관여하지 않음)를 가진다. 따라서 γ =(5+2)/5=7/5=1.4이다.
<표 1> Relation with degrees of freedom of a molecule

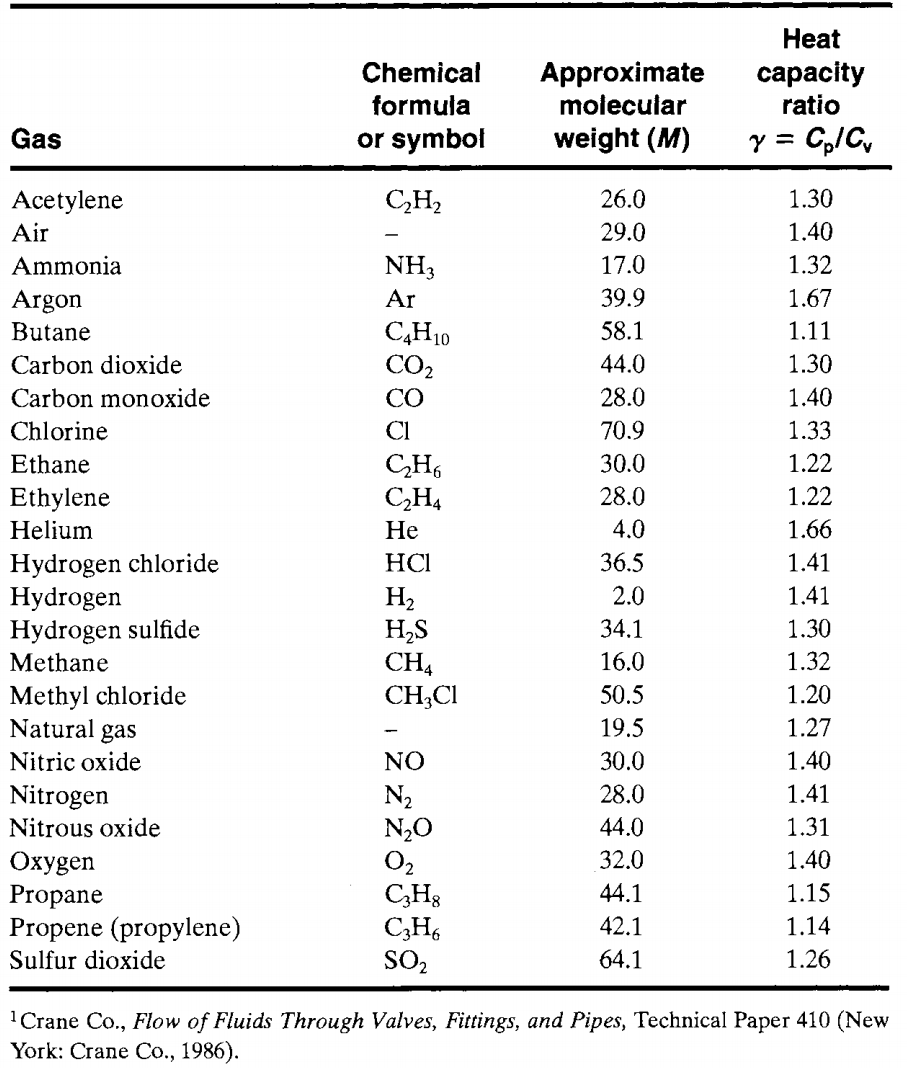
다양한 가스에 대한 열용량 비율 γ의 값은 다음 표에 예시하였다.
<표 2> Heat Capacity Ratios γ for Selected Gases
최대 질량유량 방정식
공기(air)가 대기 조건 (PChoked = 14.7psia) 으로 누출하는 경우, upstream pressure이 14.7 / 0.528 = 27.8psia 또는 13.1psig보다 크면, 흐름이 막히고(choked) 누출을 통해 최대화된다.
choked flow가 발생하는 조건은 공정 산업에서 흔히 발생한다.
따라서 최대 유량 계산식은 방정식 6을 방정식 5에 대입하여 다음 방정식 7과 같다:
(식 7)
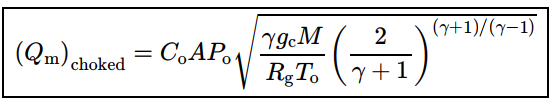
여기서

Reynolds numbers가 30,000보다 크고(쵸크 흐름이 아닌 경우) 날카로운 오리피스(sharp-edged orifices)의 경우, 일정한 배출 계수(constant discharge coefficient) Co는 0.61이다.
그러나 쵸크 흐름의 경우 다운스트림 압력이 감소함에 따라 배출 계수가 증가한다. 쵸크 흐름이거나 Co가 불확실한 상황에서는 보수적인 값인 1.0을 사용하는 것이 좋다.
계산 사례
1. 공정 조건
14barg와 25°C에서 질소가 들어 있는 탱크에 0.2cm의 구멍이 생겨 대기로 누출될 경우, 이 누출공을 통한 질량 유량을 구하라.
2. Solution
1) 쵸크 압력 (choked pressure)
- 표 2에서 질소 γ = 1.41
- 방정식 6과 Po=14 barg=14 + 1.013 = 15.01 bara.으로부터
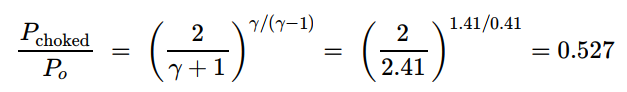
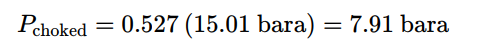
2) 질량 유량
- 외부 압력이 7.91 bara. 미만이면 누출공을 통한 흐름은 쵸크 흐름이 된다.
- 따라서 이 경우 외부 압력은 대기압(1.013bar)이므로 쵸크 흐름이 예상되며 방정식 7이 적용된다.
- 누출공 단면적
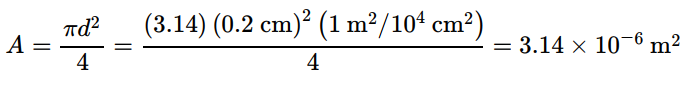
- discharge coefficient Co = 1.0
- To=25+273 = 298 K
-
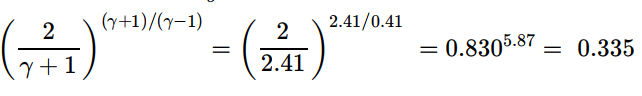
- 질량 유량

Reference : Daniel A. Crowl & Joseph F. Louvar, Chemical Process Safety Fundamentals with Applications Fourth Edition
'공학 기술 > 공학기본' 카테고리의 다른 글
| 자유 팽창(free expansion) vs. 교축(throttling) 과정 (0) | 2024.07.02 |
|---|---|
| 교축 Throttling (0) | 2024.07.01 |
| Tank 구멍을 통한 액체의 누출량 (0) | 2024.06.22 |
| 구멍을 통한 액체의 누출량 (0) | 2024.06.21 |
| 전류의 기본 개념 (0) | 2024.05.26 |


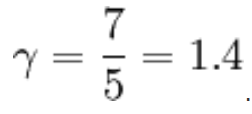




댓글