압력, 부피, 온도 변화에 따른 기체의 상태를 이상 기체 방정식으로 완전히 설명할 수 있는 가상적인 기체를 이상기체라 하고 보일 법칙, 샤를 법칙, 아보가드로 법칙을 모두 적용할 수 있는 식으로 나타낸 것을 이상 기체 상태 방정식이라 한다.

이상 기체 상태 방정식
이상 기체 법칙
보일 법칙, 샤를 법칙, 아보가드로 법칙을 모두 적용할 수 있는 식으로 나타낼 수 있다.
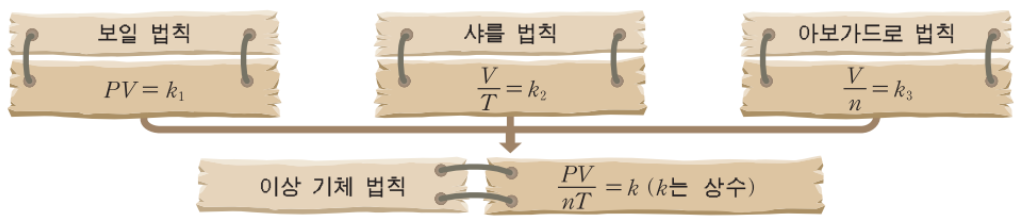
이상 기체 상태 방정식
보일-샤를의 법칙에 의하여 일정량의 기체의 PV/T = k의 값은 일정하다.(k는 기체상수 R로 표시하기도 한다.)
압력을 1atm, 온도를 ℃(273K)라 하면 1mol의 기체는 22.4ℓ의 체적을 가지고 있으므로 이 식에 대입하면 k의 값이 구해진다.

PV = RT (기체 1mol의 관계식)
또한, n mol의 기체는 표준상태에서 22.4×n(ℓ)이 되므로
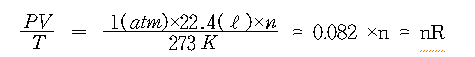
따라서, 이상 기체 n몰에 대하여 이상 기체 법칙은 다음의 식으로 나타낼 수 있다.

지금 분자량이 M인 기체(Wg)가 실존한다면, Wg은 W/M mol에 해당된다. 즉 n = W/M이 되고 이상기체법칙은 다음 식으로 나타낼 수 있다.
PV = (W/M)RT (n = W/M mol의 관계식)
기체 상수(R)
기체 1몰은 0 ℃, 1기압에서 22.4 L를 차지하므로, 이 값을 대입하여 이상 기체 법칙의 비례 상수(k), 즉 기체 상수 R을 구할 수 있다.
* 표준 온도와 압력(standard temperature and pressure, STP): 0℃, 1 atm
STP에서 실제 기체 ≒ 이상 기체. 이때 기체 1 mol의 부피 = 22.414 L
--> 일반적인 계산에서, R = 0.082 atm•L/mol•K, V = 22.4 L 값 사용.

또는
1 atm = 101325 Pa = 101325 N/m2 와 22.4 L = 0.0224 m3 를 대입해서 R을 계산하면,
R = PV / nT
= [(101325 N/m2) (0.0224 m3)] / [(1 mol) (273 K)]
= 8.314 N•m/mol•K
= 8.314 J/mol•K
( 1 N•m = 1 J )
▶ 기체상수의 단위를 보면 알 수 있듯이, 기체의 압력 및 부피 변화와 관련된 문제에서는 0.08206 을
기체의 에너지 변화와 관련된 문제에서는 8.314 를 사용한다.
( 즉, 열역학 함수와 관련된 문제에서는 8.314 를 사용. )
표준 조건(Standard conditions) vs. 표준 상태(Standard state)의 다음 포스팅 참조
https://sec-9070.tistory.com/46
표준 조건(Standard conditions) vs. 표준 상태(Standard state)
표준 조건(Standard conditions) 즉 STP와 표준 상태(Standard state)는 둘 다 과학적 계산에 사용되지만, 항상 같은 것을 의미하지는 않는다. 표준 조건(Standard conditions) vs. 표준 상태(Standard state..
sec-9070.tistory.com
'공학 기술 > 공학기본' 카테고리의 다른 글
| 정유공정 및 NCC공정 (0) | 2021.02.27 |
|---|---|
| 석유화학공업 체계도 (0) | 2021.02.27 |
| 온도(Temperature)와 압력(Pressure) (0) | 2021.02.02 |
| 몰(Mole) 과 농도(Concentration) 관계 (0) | 2021.02.02 |
| 일, 에너지, 일률(동력) 개념 (0) | 2021.02.02 |





댓글